[ Список научных сотрудников ]

Лаборатория теории нелинейных процессов была основана в 1973 проф. Г.М. Заславским. Основной темой теоретических исследований тогда был хаос в нелинейных классических системах. В настоящее время лабораторией  руководит д.ф.-м.н., профессор Алмаз Фаттахович Садреев

О сновные направления исследований за 2003—2008 гг.:

1. Квантовый хаос и его приложения в квантовой оптике и открытых резонаторах и упругих биллиардах.
2. Волновой транспорт в линейных и нелинейных системах.
3. Осцилляции Блоха и проблема Ванье-Штарка.
4. Нелинейная динамика Бозе-Эйнштеновских конденсатов.
5. Прохождение света в фотонно-кристаллических волноводах, связанных с оптическими керровскими полостями с упором на само индуцированные связанные состояния в континууме, т.е., на локализацию света.

В перечисленные ниже работы включены наиболее значимые результаты научной деятельности лаборатории:

1. Рассмотрен аналог эффекта Холла в 4-х терминальной гетероструктуре за счет спин-орбитального взаимодействия Рашба (E.N.Bulgakov, K.N.Pichugin, A.F.Sadreev, P.Seba and P.Streda, Phys. Rev. Lett. 83, 376-380 (1999); K.N.Pichugin, P.Streda, P.Seba and A.F.Sadreev, Physica E 6, 727-730 (2000)).
2. Доказано, что не существует спиновой поляризации в двухтерминальной гетероструктуре со спин-орбитальным взаимодействием Рашба, если электронный транспорт является одноканальным (E.N.Bulgakov and A.F.Sadreev, Phys. Rev. B 66, 075331 (2002)). Результат был подтвержден в других публикациях других авторов.
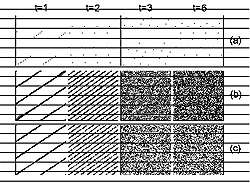
3. Сформулирован количественный критерий соответствия между классической и квантовой динамикой хаотической системы (A.R. Kolovsky, Phys. Rev. Lett. 76, 340 (1996)). Эволюция функции Вигнера для квантового отображения Арнольда показана На Рис. 1.

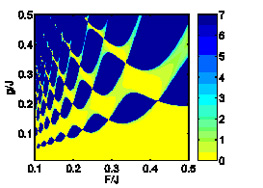Рис. 1. Эволюция функции Вигнера для квантового отображения кота Арнольда, в случае когда условия соответствия не удовлетворены, и удовлетворены соответственно. Последний ряд: эволюция функции распределения для классического отображения кота Арнольда.	Рис. 2. Количество конденсированных Бозе атомов, совершающих осцилляции Блоха, как функция межатомного взаимодействия и амплитуды внешнего статического поля.

4. Решена проблема Ванье-Штарка о метастабильных состояниях квантовой частицы в периодическом потенциале, под действием внешнего статического поля (M. Gluck, A.R. Kolovsky, H.J. Korsch, Physics Reports, 366, 103 (2002)).
5. Решена задача об осцилляциях Блоха конденсата холодных бозе атомов в оптических решетках (Kolovsky, AR; Korsch, HJ; Graefe, EM Phys. Rev. A, 80 023617 (2009)).
6. Развита теория связанных состояний в континууме в открытых двумерных биллиардах, двойных биллиардах, Ааронов-Бомовских кольцах и фотонно-кристаллических волноводах, связанных с двумя оптическими резонаторами (I. Rotter and A.F. Sadreev, Phys. Rev. E 71, 046204 (2005). E.N. Bulgakov, K.N. Pichugin, A.F. Sadreev, and I. Rotter, JETP Letters, 84, 430 (2006); A.F. Sadreev, E.N. Bulgakov, and I. Rotter, Phys. Rev. B 73, 235342-5 (2006); E.N. Bulgakov, I. Rotter, and A.F. Sadreev, Phys. Rev. A 75, 67401 (2007); глава в книге "Quantum Dots, Research, Technology and applications", ed. By R.W. Knoss, pp. 547-577 (2008, Nova Sciencers Publ.); A.F. Sadreev, E.N. Bulgakov, K.N. Pichugin, I. Rotter, and T.V. Babushkina, Transmission through quantum dots with variable shape. Bound states in the continuum; E.N. Bulgakov and A.F. Sadreev, Phys. Rev. B78, 075105-8 (2008)). Интерес к связанным состояниям в континууме прежде всего вызван тем, что предлагается интерфереционный механизм локализации примесных состояний в зоне проводимости, если рассматривать задачу в рамках модели Фано-Андерсона. В приложении к фотонно-кристаллическому волноводу, связанного с двумя дефектами, это означает локализацию света в окрестности дефектов. Примеры таких локализованных решений для света в фотонно-кристаллтческом волноводе опубликованы в Kaleidoscope Phys. Rev. B, август 2008.
7. Само индуцированная локализация света в фотонно-кристаллическом волноводе, связанного с оптическим керровскими полостями (E.N. Bulgakov and A.F. Sadreev, Resonance induced by a bound state in the continuum in a two-level nonlinear Fano-Anderson model, Phys. Rev. B80, 115308-7 (2009); E.N. Bulgakov and A.F. Sadreev, Bound states in photonic Fabry-Perot resonator comprised of two nonlinear off-channel defects, Письма в ЖЭТФ, 90, 842-847 (2009); E.N. Bulgakov and A.F. Sadreev, Bound states in photonic Fabry-Perot resonator with nonlinear off-channel defects, Phys. Rev. B 81, 115128-12 (2010); E.N. Bulgakov, K.N. Pichugin, and A.F. Sadreev, Symmetry breaking for transmission in photonic waveguide coupled with two off-channel nonlinear defects, accepted for publication in, Phys. Rev. B83, (2011); E.N. Bulgakov, K.N. Pichugin, and A.F. Sadreev, Light induced Josephson like current between two coupled nonlinear cavities coupled aside with photonic crystal waveguide J. Phys. C23 (2011)).Среди многих результатов этого перспективного направления можно выделить следующие. 1) По крайней мере два разных керровских нелинейных дефекта, которые подкачиваются светом, распространяющегося по линейному волноводу, приводят к само-индуцированной локализации света, примерно такого же вида, что показано на Рис. 3. 2) Это локализованное состояние в силу отсутствия принципа линейной суперпозиции вызывают дополнительные резонансы, показанные на Рис. 4. 3) Если одинаковые дефекты расположены симметрично, имеет место спонтанное нарушение симметрии как по интенсивности света на дефектах, так и по фазе колебаний электромагнитного поля на дефектах. Последнее приводит к аналогу эффекта Джозефсона для тока мощности, который показан на Рис. 5.

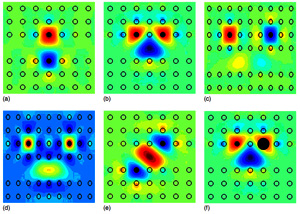Рис. 3. Примеры связанных состояний в двумерном фотонном кристалле, сфабрикованного из цилиндров GaAs с радиусом 0.18а и диэлектрической проницаемостью 11.56, показанные светлыми кружками. Волновод создан простой выемкой стержней. Дефекты показаны черными кружками и имеют диэлектрическую проницаемость 2.7406 на частоте ωa/2πc=0.3557 (a), 3.086 на частоте ωa/2πc=0.3753 (и)-(в), 2.5646. на частоте ?a/??c=0.3557 (е). (f) дефекты разные: слева с радиусом 0.18a и ? =0.8576; справа с радиусом 0.45a и ?=3.1348. Рисунки взяты из E.N. Bulgakov and A.F. Sadreev, Phys. Rev. B 78, 075105 (2008).



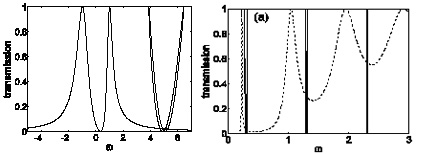
Рис. 4. Слева: трансмиссия в волноводе связанного с двумя нелинейными дефектами, расположенными продольно волноводу (из статьи E.N. Bulgakov and A.F. Sadreev, Phys. Rev. B. B80, 115308 (2009); Справа: в схеме резонатора Фабри-Перо (из статьи , E.N. Bulgakov and A.F. Sadreev, Phys. Rev. B81, 115128 (2010)).



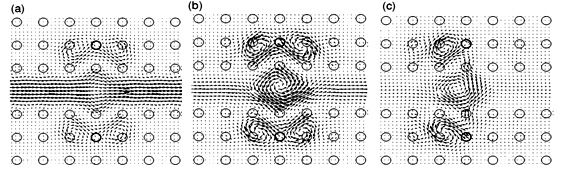
Рис. 5. Потоки мощности света (вектор Умова-Пойнтинга), распростраяющего по волноводу фотонного кристалла, вблизи которого расположены два идентичных керровских дефекта (показанные жирными кружками). (а) симметрия не нарушена; (b) симметрия нарушена по интенсивности света на дефектах и (с) симметрия нарушена по фазам колебаний на дефектах. Отчетливо видны токи между дефектами (ток Джозефсона) в случае разных фаз между дефектами.

8. Показано, что спинорный бозе-эйнштеновский конденсат в магнитной ловушке Иоффе-Питчарда может быть вихревым в основном состоянии (E.N. Bulgakov and A.F. Sadreev, Phys. Rev. Lett. 90, 200400 (2003)).
9. Движение молекул внутри узких нанотрубках под воздействием температурных флуктуаций стенок трубки. Основа для молекулярных моторов под воздействием температурного градиента вдоль трубки (A.S. Fedorov and A.F. Sadreev, Thermoactivated transport of molecules H2 in narrow single-wall carbon nanotubes, Eur. Phys. J. B 69, 363-368 (2009)).
10. Развита теория квантового хаоса в приложении к хаотическим упругим биллиардам (D.N. Maksimov and A.F. Sadreev, Gaussian random waves in elastic media, Письма в ЖЭТФ, 86, 584-588 (2007); D.N. Maksimov and A.F. Sadreev, Phase correlation function of complex random Gaussian fields, Eur. Phys. Lett., 80, 50003 (2007). Maksimov and A.F. Sadreev, Statistics of nodal points of in-plane random waves in elastic media, Phys. Rev. E77, 056204-7 (2008)).

Работы лаборатории по исследованию признаков хаоса в открытых системах вошли в достижения Института за 2002 год.