|
1992-1996;
1997;
1998;
1999;
2000;
2001;
2002;
2003;
2004;
2005;
2006;
2007;
2008;
2009

Теоретические исследования

Исследован спектр волн в синусоидальной сверхрешетке, содержащей одно или трехмерные неоднородности периода сверхрешетки. Впервые такое исследование проведено с учетом точных корреляционных функций, справедливых для любых величин среднеквадратичных флуктуаций неоднородностей. Получена резкая зависимость амплитуд и ширин линий резонансных пиков на границе 1-ой зоны Бриллюэна сверхрешетки от размерности неоднородностей положения и структуры интерфейсов.
Для описания спектра волн в частично стохастизованной сверхрешетке с конечной толщиной интерфейсов введена модель, в которой зависимость материального параметра вдоль оси сверхрешетки описывается эллиптической функцией со случайно модулированным периодом. Выведена корреляционная функция такой модели. Исследован закон дисперсии и затухание усредненных спиновых волн в такой сверхрешетке. Получены зависимости ширины щелей в спектре и затухания на границах всех нечетных зон Бриллюэна сверхрешетки от толщины интерфейсов, интенсивности и корреляционных свойств одномерных неоднородностей.
- Ignatchenko V. A., Erementchouk M. V., and Maradudin A. A. Correlation-induced coupling of wave fields in disordered media. Phys. Rev. B, 2001, 63, 54205.
- Ignatchenko V. A., Mankov Yu. I., and Maradudin A. A. Spin-wave spectrum in partially randomized multilayers with finite thickness of interfaces. Phys.Met.Metallogr, 2001, 91, 1, .
- Ignatchenko V. A., Maradudin A. A., and Pozdnyakov A. V. Spin-wave susceptibility of partially disordered multilayers. Phys.Met.Metallogr, 2001, 91, 1, 69.
Работы выполнены при поддержке NATO Collaborative Grant № 978090, гранта РФФИ № 00-02-16105,
Исполнитель - лаборатория теоретической физики,
Зав. лаборатории - д.ф.-м.н. В. А. Игнатченко.
Решена проблема построения однозначного алгоритма последовательного применения теоремы Вика для вычисления термодинамических средних от хронологизированных по мацубаровскому времени произведений операторов Хаббарда. Предложенный алгоритм основан на введении двух принципов: принципа топологической непрерывности и старшинства линий взаимодействия. Эти принципы позволяют однозначно выбирать производящий оператор на каждом шаге применения теоремы Вика и заменяют используемый ранее принцип иерархии недиагональных операторов Хаббарда. Преимущества нового подхода особенно заметны при развитии теории сильнокоррелированных систем с произвольно большим числом одноячеечных состояний, поскольку в этом случае использование принципа иерархии становится практически невозможным. Сформулированы правила записи аналитических выражений для произвольных диаграмм и выведены уравнения Ларкина и Дайсона. Показано, что предложенная форма записи матричных элементов взаимодействия в атомном представлении, имеющая явно расщепленный характер, позволяет радикально упростить решение системы большого числа уравнений при нахождении функций Грина. Данное обстоятельство имеет существенное значение при исследовании систем с большим числом одноячеечных состояний в атомном представлении. Конкретное использование развитой формы диаграммного описания продемонстрировано на нескольких моделях сильнокоррелированных систем.
- Вальков В.В., Овчинников С.Г. "Квазичастицы в сильнокоррелированных системах".
Издательство СО РАН, Новосибирск, 2001, 278с.
Изучен спектр элементарных возбуждений двумерного анизотропного негейзенберговского антиферромагнетика. Анизотропия кубической симметрии учитывалась посредством введения трех инвариантов, описывающих четырехспиновое обменное взаимодействие. При учете квантовых флуктуаций определены области устойчивости фаз [100], [111] и [110]. Показано, что фаза [110] является неустойчивой. Найдены смещения границ раздела фаз [100] и [111] за счет квантовых флуктуаций.
Точное решение уравнений Горькова для модельного потенциала спаривания позволило проанализировать эффект Джозефсона в условиях резонансного туннелирования и произвольных значениях температур для слоистой структуры SISIS. Показано, что сверхток Джозефсона представляется в виде суперпозиции двух составляющих, каждое из которых имеет различную асимптотику при 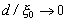 (d - толщина диэлектрического слоя, (d - толщина диэлектрического слоя, 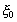 - длина когерентности) и при - длина когерентности) и при 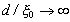 . Существенно, что эти составляющие немонотонным образом зависят от отношения . Существенно, что эти составляющие немонотонным образом зависят от отношения 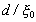 и описывают эффекты резонансного туннелирования. и описывают эффекты резонансного туннелирования.
Проведено развитие диаграммной техники для спиновых операторов, позволившее описывать упорядоченные магнетики с развитыми нулевыми квантовыми колебаниями. Исследованы спектральные свойства низкомерных антиферромагнетиков в скошенной фазе в магнитном поле.
Для слабодопированной квазидвумерной системы с сильными электронными корреляциями и прямым антиферромагнитным обменом исследована роль электрон-фононного взаимодействия на формирование сверхпроводящего состояния. При выводе эффективного гамильтониана использовался метод канонических преобразований. Показано, что учет фононной подсистемы приводит к дополнительному обменному взаимодействию, которое не зависит от температуры, а также к перенормировке электронных перескоков, сильно возрастающей при T~50-100K. Указанные процессы сказываются на величине критической температуры сверхпроводящего перехода и ее концентрационной зависимости. Проанализировано влияние электронных перескоков на вторые соседи при учете смещения особенности ван Хова. Установлено, что в рамках развиваемой теории такое смещение не может привести к изменению симметрии сверхпроводящего параметра порядка, но может дать уширение концентрационного интервала существования сверхпроводимости.
Для изотропной модели Гейзенберга со спином s=1/2 на квадратной решетке и антиферромагнитным обменным взаимодействием между ближайшими соседями рассмотрено термодинамически устойчивое состояние, названное спиновой жидкостью (SL). SL состояние пространственно однородно, характеризуется нулевыми средними на узле решетки для любой компоненты спинового оператора и изотропными спиновыми корреляционными функциями. Описание системы проведено методом двухвременных температурных функций Грина, построенных на спиновых операторах, в рамках теории 2-го порядка. Предложен новый способ получения замкнутой системы уравнений для самосогласованного вычисления температурно зависящих параметров модели. Показано, что SL состояние при температуре T —> 0 переходит в синглетное состояние с энергией (на связь в единицах обмена) 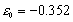 , которая ниже энергии антиферромагнитного (AF) состояния; корреляционная длина в этом пределе расходится. Пространственные спиновые корреляторы знакопеременны (как и в AF состоянии) и убывают с ростом температуры и расстояния. Вычислены основные характеристики системы: теплоемкость, параметр "жесткости" спектра возбуждений, магнитная восприимчивость, корреляционная длина и др. во всем температурном диапазоне. , которая ниже энергии антиферромагнитного (AF) состояния; корреляционная длина в этом пределе расходится. Пространственные спиновые корреляторы знакопеременны (как и в AF состоянии) и убывают с ростом температуры и расстояния. Вычислены основные характеристики системы: теплоемкость, параметр "жесткости" спектра возбуждений, магнитная восприимчивость, корреляционная длина и др. во всем температурном диапазоне.
Исследован электронный энергетический спектр тяжелофермионных антиферромагнетиков с металлическим типом основного состояния в магнитном поле в скошенной фазе. Показано, что энергетическая структура скошенного тяжелофермионного антиферромагнетика качественно отличается от зонной структуры парамагнитной фазы и характеризуется наличием четырех щелей. Проанализирована трансформация плотности состояний тяжелых фермионов при изменении внешнего магнитного поля.
Предложен метод, позволяющий исключать вклады от неортогональности электронных состояний, связанных с туннельными структурами. Теория применена для описания однобарьерной туннельной структуры. Получено простое выражение для зависящего от времени туннельного тока, показывающего явную связь с перекрытием. Развитая теория воспроизводит экспериментальные результаты значительно лучше, чем стандартные подходы.
Результаты получены при поддержке Федеральной целевой программы "Интеграция", грант А0019 и РФФИ, гранты № 99-02-7405, № 00-02-1610.
Исполнители:
лаборатория теории твердого тела, зав. лаборатории -
д.ф.-м.н. В. В. Вальков
лаборатория физики магнитных явлений, зав. лаборатории -
д.ф.-м.н. С. Г. Овчинников.
Хорошо известно, что для замкнутых квантовых хаотических систем статистические свойства энергетических уровней описываются теорией случайных матриц (ТСМ). В этом подходе предполагается, что гамильтониан может быть представлен в виде матрицы со случайными элементами, распределенными по Гауссу. Этот подход может быть использован и для открытых систем, добавляя мнимые части в соответствующие матричные элементы гамильтониана.
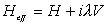
Этот способ адекватно описывает распределение комплексных волновых функций в интервале l от нуля до единицы. Однако в целом ТСМ подход является крайне сложным для расчетов. В нашем методе при изучении электронного и микроволнового транспорта через хаотические биллиарды мы предлагаем использовать упрощенные волновые функции рассеяния
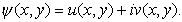 (1) (1)
Эти функции обязаны быть комплексными и удовлетворяют уравнению Наше предположение состоит в том, что эти функции u и v являются случайными гауссовскими полями, которые зависят друг от друга. Тем не менее, фазовое преобразование
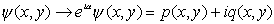 (2) (2)
приводит к новым также распределенным по Гауссу полям p и q, которые являются статистически независимыми и по этой причине
более пригодны для вычисления параметра
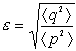 (3). (3).
Кроме того, выполняется
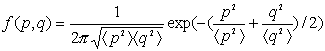 (4). (4).
Таким образом, попутно мы воспроизводим стандартные аналитические формулы для статистики волновых функций полученные в рамках теории случайных матриц. Кроме того, дополнительно к этим хорошо известным результатам мы получаем и новые распределения для волновых функций (2) и (4) плотности тока (вектор Умова-Пойтинга в случае электромагнитных волн).
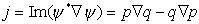 (5). (5).
Для компонент тока
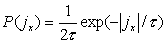 (6) (6)
и для абсолютных значений
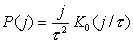 (7) (7)
где 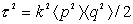 . .
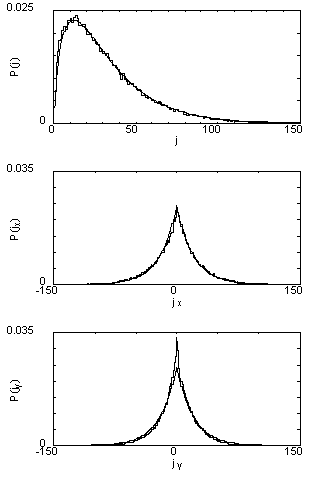
Аналитические результаты сравниваются с численными в случае электронного транспорта через стадионы Бунимовича и Синая (см. рисунок). Как видно из рисунка, согласие теории с численным экспериментом прекрасное. Более того, наши основные результаты по статистике распределения токов нашли полное подтверждение в экспериментах M. Barth и H.-J.Stockmann из Германии по переносу электромагнитного излучения через биллиард Робника.
|
| Функция распределения плотности тока P(j) (вверху) и ее компоненты P(jx) и P(jy) (в середине и в низу) в открытом биллиарде
|
- Ishio H., Saichev A. I., Sadreev A. F., and Berggren K.-F., Wave Function Statistics for Ballistic Quantum Transport through Chaotic Open Billiards: Statistical Crossover and Coexistence of Regular and Chaotic Waves, Phys. Rev. E , 2001, 64, 056208-1-12.
Аналитически и численно изучены статистические свойства тока для двумерных хаотических открытых баллистических биллиардов. Предполагая, что вещественная и мнимая часть волновой функции рассеяния заданы случайными значениями с Гауссовым распределением, мы получили аналитически функцию распределения для токов и их компонент. Попутно мы воспроизвели известные ранее статистические свойства волновых функций. Наши аналитические результаты сравниваются с численными квантово-механическими исследованиями баллистического переноса для биллиарда Бунимовича. Хорошее качественное соответствие между численным и аналитическим подходами дают основание для теоретического подхода к исследованию переходной области между открытыми и закрытыми хаотическими системами. Возможность наблюдения токовых распределений в микроволновых биллиардах отмечается.
Прямоугольные микроволновые резонаторы, заполненные ферритом с одноосной магнитной анизотропией, рассмотрены. Строго показано, что задача сводится к исследованию пустого резонатора в форме ромба с углом при вершине, определяемым внешним магнитным полем, порожденным магнитной анизотропией феррита. Статистика собственных частот ТМ мод описывается распределением Brody или semi-Poisson.
Анализ квантового хаоса в терминах сечения Пуанкаре, полученного с помощью Хусими функций для когерентного транспорта через хаотические биллиарды.
Разработан комплекс программ для вычисления и визуализации функций Хусими для квантовых систем с произвольной геометрией.
Используя тот факт , что действительная и мнимая части волновой функции Берри являются случайными гауссовыми полями , корреляционная функция и плотность нодальных точек рассмотрены. Вычислена функция распределения ближайших расстояний между нодальными точками и ее основные ассимптотики. Результаты аналитических исследований хорошо совпадают с результатами численного эксперимента.
Энергия активации молекул, адсобированных на поверхности кристалла, определяется потенциалом взаимодействия. Величина этого потенциала уменьшается за счет взаимодействия адсобированных молекул с фононами кристалла. Учет ротационных степеней свободы молекул относительно кристаллической поверхности также приводит к уменьшению энергии активации. В нашем случае были рассмотрены молекулы (C6H11)3P, адсобированные на поверхности кристалла родия. Взаимодействие молекул родия и трициклогексилфосфана описывались потенциалом Морса, параметры которого были выбраны с учетом экспериментальных данных. Проведено сравнение теоретической зависимости энергии активации от температуры, полученной на основе уравнения Редхеда, с результатами TPD (temperature-programmed desorption) экспериментов
Работы выполнены при поддержке грантов Академии наук Швеции и гранта РФФИ № 01-02-16077.
Исполнитель - лаборатория теории нелинейных процессов,
Зав. лаборатории - д.ф.-м.н. А. Ф. Садреев.
|