
Показано, что ССК (связанные состояния в континууме) может быть реализовано в квантовом транспорте через специальную систему двух дотов связанных проволокой

Обычно решения уравнения Шредингера с локальным потенциалом 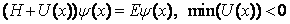 являются дискретными для отрицательных энергий и непрерывными для положительных энергий. Соответственно решения являются локализованными или связанными для Е < 0 и размазанными по всему пространству для E > 0. В 1929 г. фон Нейман и Вигнер предположили, что могут существовать и дискретные положительные уровни энергии с локализованными функциями (связанные состояния). Им были найден ряд конкретных потенциалов, имеющих связанные состояния в континууме (ССК). являются дискретными для отрицательных энергий и непрерывными для положительных энергий. Соответственно решения являются локализованными или связанными для Е < 0 и размазанными по всему пространству для E > 0. В 1929 г. фон Нейман и Вигнер предположили, что могут существовать и дискретные положительные уровни энергии с локализованными функциями (связанные состояния). Им были найден ряд конкретных потенциалов, имеющих связанные состояния в континууме (ССК).
Результаты фон Неймана и Вигнера стимулировали значительный теоретический и экспериментальный интерес к ССК (см., например, недавнюю работу L.S. Cederbaum, et al, Phys. Rev. Lett. 90, 13001 (2003)). В частности, в работе H. Friedrich and D. Wintgen, Phys. Rev. A31, 3964 (1985) был найден ССК в атоме водорода в сильном магнитном поле. Эти же авторы пришли к заключению, что условие реализации ССК может существенно облег-читься в многомерном случае уравнения Шредингера.
Здесь мы показываем, что ССК может быть реализовано в квантовом транспорте через специальную систему двух дотов связанных проволокой. Особенность системы состоит в том, что проволока может непрерывно менять длину L или ширину W, так что ее собствен-ные уровни энергии пересекают уровни энергии дотов, как показано на Рис. 3.
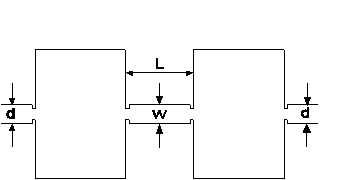
Рис. 3. Схема квантового транспорта через систему двух идентичных биллиардов, связанных квантовой проволокой с переменными размерами
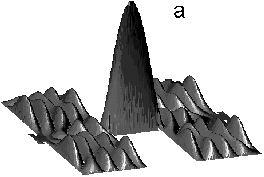
Рис. 4. Амплитуда волновой функции рассеяния. Вероятность найти частицу в проволоке на два порядка превышает вероятности в биллиардах. В подводящих электродах вероятность равна нулю: так называемое связанное состояние в континууме.
Показано как аналитически, так и численно, когда уровень энергии проволоки пересекает линию нулей трансмиссии полной системы, возникает связанное состояние с нулевой шириной линии. Это означает, что новое связанное состояние локализовано внутри квантовой системы и имеет дискретный уровень энергии, расположенным внутри континуума.
Кроме того, оказалось, что пространственная структура ССК является чрезвычайно чувствительной к пределу к особой точке, определенной как пересечение энергии проволоки с нулем трансмиссии, а также к силе связи системы с электродами. В частности для малой связи системы с электродами, электрон локализуется внутри проволоки, явление невозможное для закрытой системы (Рис. 4).
- A.F. Sadreev, E.N. Bulgakov, and I. Rotter, Trapping of an electron in the transmission through two quantum dots coupled by a wire, Письма в ЖЭТФ, 82, 56-561 (2005).
- A.F. Sadreev, E.N. Bulgakov, and I. Rotter, S-matrix formalism of transmission through two quantum billiards coupled by a waveguide, J. Phys. A: Math. Gen. 38, December (2005).
Лаборатория Теории Нелинейных Процессов
|