
Теоретические исследования пространственных структур, энергетического спектра, динамических и кинетических свойств магнитных материалов и мезоскопических полупроводниковых структур; разработка математических методов и программных средств обеспечения проводимых исследований

Показано, что в Бозе-эйнштейновском конденсате магнитное поле магнитной ловушки Иоффе-Притчарда образует вихри в компонентах спинорного конденсата, находящегося в основном состоянии. Найдена фазовая диаграмма (рис. 1) существования вихрей в осях поперечное и продольное магнитное поле. Найдена область на фазовой диаграмме, в которой вихри пространственно разделяются. Механизм образования вихрей является совершенно новым и связан с особой пространственной конфигурацией магнитного поля, действующего на конденсат.
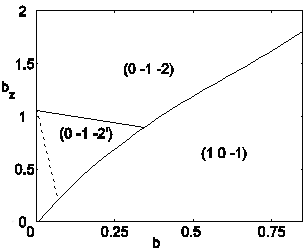
Рис.1 Фазовая диаграмма бозе конденсата в осях поперечно-продольное магнитное поле.
Впервые найдена схема аналитического расчета матрицы связи закрытого биллиарда с двумя и более присоединенными волноводами. Это позволяет вычислить матрицу рассеяния и полюса этой матрицы как комплексные собственные значения неэрмитового эффективного гамильтониана для задач транспорта через биллиарды и сопоставить эти полюса с пиками проводимости биллиарда.
Рассмотрена статистика собственных волновых функций хаотического биллиарда с учетом спин-орбитального взаимодействия Рашбы. Вопреки ожиданиям, основанным на предсказаниях теории симплектических случайных матриц, одна компонента собственных функций удовлетворяет статистике Гаусса, тогда как статистика второй компоненты не является универсальной и зависит от конкретной формы биллиарда при малой константе спин-орбитальной связи. В пределе большой константы спин-орбитальной связи обе компоненты описываются гауссовскими распределениями.
Изучены спектральные и динамические свойства холодных безспиновых атомов в 1D оптической решетке в рамках формализма Бозе-Хаббарда.
Показано, что при определенных условиях статистические свойства системы могут описываться в рамках гауссовского ортогонального ансамбля.
Работы выполнены при поддержке:
- Грантов РФФИ № № 01-02-16077, 03-02-17039
- Гранта Шведской Академии наук
Лаборатория теории нелинейных процессов
|