Как
обрабатывать результаты опыта
Чтобы
строить гистограмму и сравнивать ее форму с функцией
Гаусса, нужно повторять измерения сотни раз. Так
делают очень редко. Как правило, главные
характеристики гауссова распределения (среднее
значение Хо и стандартное отклонение (7) вычисляют из небольшого
числа данных. Результаты расчетов, сделанных на
основе 5 или 7 измерений, могут отличаться от результатов
расчета тех же параметров
x0
и
σ,
которые можно вычислить, зная данные 100 или 1000 измерений, но
таким различием часто пренебрегают.
Повторим
измерение одной величины х несколько раз (
n
раз). Результаты измерений будем обозначать х
1,
x
2,
x
3,
..., x
n.
Среднее значение
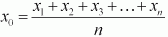 . (10) . (10)
Стандартное
отклонение результатов опыта от среднего значения
σ
вычисляют по формуле
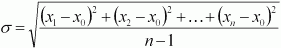 . (11) . (11)
Почему
в формуле (11) стоит в знаменателе
n–1
вместо
n?
Оказывается, что при небольших
n
такая формула дает лучшую оценку стандартного
отклонения, чем формула с
n
в знаменателе. А если сделан один опыт, в формуле (11)
получается «ноль, деленный на ноль»: и это
напоминает нам о невозможности вычислить стандартное
отклонение по результатам единственного измерения.
Рассмотрим
пример расчета. Измеряя время движения тела по наклонной
плоскости, школьник получил результаты: 7, 5, 4, 5, 6, 3 секунды. Среднее
время:
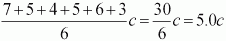 . .
Стандартное
отклонение:
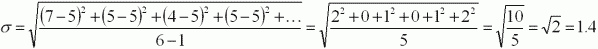
Итак,
время равно (5.0±1.4)с. Отметим, что в промежуток от (5.0–1.4)с
до (5.0+1.4)с, т.е. от 3.6 до 6.4с, попадают не все результаты
измерений, а только 4 из 6 (результаты 3 и 7 с лежат вне этого
промежутка). Этого и следовало ожидать: около 2/3 опытов должно
попасть в промежуток от
x0–σ
до
x0+σ.
Выводы.
Среднее значение
x0
и стандартное отклонение
σ
можно легко вычислить по результатам нескольких измерений.
Результат
единственного измерения не позволяет определить стандартное отклонение.
|