Äèíàìèêà àòîìíîãî îñòîâà è ýëåêòðîííàÿ ñòðóêòóðà ðÿäà ýíäî- è ýêçîýäðàëüíûõ êîìïëåêñîâ ôóëëåðåíà ñ ëåãêèìèì ýëåìåíòàìè
П.В. Аврамов1,3, С.А. Варганов1, С.Г. Овчинников1,2,3
1Институт физики им. Л.В. Киренского СО РАН, 660036, Красноярск
2Красноярский государственный технический университет
3Красноярский государственный университет
e-mail: [email protected]
Набором полуэмпирических и неэмпирическим квантово-химическим методом были исследованы атомная и электронная структуры ряда эндо-, экзо- и эндо-экзоэдральных комплексов фуллерена С60 с различными атомами и молекулами-гостями (Hen, H2, Li2). Динамика атомного остова исследовалась методом неэмпирической молекулярной динамики. Показано, что уже при достаточно низких температурах (от 4 до 78К) атомы и молекулы-гости, находящиеся внутри фуллереновых сфер, приобретают орбитальный момент за счет коррелированного движения ядер над низкоэнергетическими барьерами потенциальной поверхности внутри углеродной сферы. Возникновение орбитальных моментов ядер атомов и молекул-гостей объяснено изменением вклада орбитального электронного момента в потенциальную поверхность комплексов. Движение ионов Li внутри сферы приводит к размыванию потолка валентной зоны и к появлению волны зарядовой поляризации углеродной сферы.
PACS: 61.46.+w

Введение

В настоящее время известно уже большое количество соединений фуллерена с металлами (см., например [1-3]). Все это многообразие делится на два больших класса - эндоэдральные комплексы, когда атомы металла находятся внутри фуллереновых сфер, и экзоэдральные - когда атомы металла находятся снаружи. Оба класса привлекают к себе пристальное внимание исследователей своими уникальными химическими и физическими свойствами, в частности - магнитными и сверхпроводящими. В настоящее время пожалуй самыми интересными металло-фуллереновыми объектами являются экзо- и эндоэдральные комплексы фуллеренов со щелочными металлами. Это объясняется прежде всего тем, что соединения типа K3C60 и Rb3C60 [1, 4] являются сверхпроводниками с достаточно высокими температурами сверхпроводящего перехода, доходящими до 55К. В последнее время был также разработан и элегантный способ синтеза эндоэдралов Li@C60, Li2@C60 и Li3@C60, заключающийся в том, что фуллерит C60 облучается пучком ионов лития с энергией до 30 эВ [5].
Комплексы фуллеренов с металлами интенсивно и уже достаточно долго изучаются как экспериментальными (см., например, [5-12]), так и теоретическими (см., например [1, 3, 13-27]) методами. Методами электронной спектроскопии исследовалась электронная структура металлокомплексов. Так, в [9] исследовались фотоэлектронные спектры и спектры обращенной фотоэмиссии экзоэдральных соединений типа KxC60 (Рис. 1 [9]). Как видно, заполнение нижней вакантной орбитали С60 при допировании щелочным металлом (в данном случае - калием) приводит не только к смещению занятых и вакантных состояний, но и к существенному изменению формы полос и сложному поведению уровня Ферми. Переход от чистого C60 к KC60 приводит к исчезновению запрещенной щели за счет возникновения внедренного состояния с одной стороны и существенного (порядка 1 эВ) смещения первой особенности спектра обращенной фотоэмиссии - с другой. Дальнейшее повышение степени допирования приводит к монотонному увеличению плотности внедренного электронного состояния, тогда как вакантное состояние ведет себя более сложно - при степени Быстрая миграция иона La внутри фуллереновой сферы была изучена и в методе молекулярной динамики на основе потенциала, полученного в LDA-подходе [33]. Было показано, что La очень быстро тангенциально двигается относительно углеродной сферы и совершает один оборот примерно за одну пикосекунду. Аналогичные результаты были получены авторами [33, 34] и для эндоэдрала La@C82. Эти результаты позволили сделать вывод, что ряд экспериментов по электронной и атомной структуре необходимо интерпретировать по другому, с учетом вращения. Так, в частности, спектроскопией ЭПР становится невозможно извлекать необходимую информацию, так как характерные времена для ЭПР-процессов на порядок больше, нежели чем период вращения иона лантана внутри сферы.
В настоящее время уже известно достаточно большое количество эндоэдральных комплексов фуллеренов как с индивидуальными атомами, так и с некоторыми молекулами. Очевидно однако, что не все атомы и молекулы-гости могут двигаться внутри углеродных сфер. Несмотря на то, что на эти экзотические соединения было обращено пристальное внимание как экспериментаторов, так и теоретиков, в частности, вопрос - о способе координации атомов и молекул-гостей, которые остаются неподвижными внутри сферы, в общем виде так и не был решен. Действительно, до настоящего времени были получены лишь единичные экспериментальные сведения о структуре твердых тел на основе эндоэдралов, как например структура Y@C60, для которого известно [10], что атом иттрия жестко прилеплен изнутри к углеродной стенке, а сами эндоэдральные молекулы в молекулярном твердом теле координированы способом «голова к хвосту».
По вполне понятным причинам, в теоретическом плане способы координации атомов - гостей изучены в настоящее время гораздо лучше, нежели чем в экспериментальном. Было показано, что некоторые атомы и ионы, к примеру He, K+ [16, 17, 25], должны координироваться в центре углеродной сферы, а некоторые другие, такие, как Li+, Na+ - около углеродной стенки [13, 16, 37]. Из самых общих положений ясно, что для одного атома-гостя существует 5 способов координации (к центрам шестиугольника, пятиугольника, ребра шестиугольник-шестиугольник, ребра пятиугольник-шестиугольник и к вершине усеченного икосаэдра). Очевидно, что при наличии более одного атома-гостя способов координации внутри углеродной сферы может быть еще больше.
Необходимо отметить интересную с теоретической точки зрения работу [14], в которой было показано, что атомы-гости могут туннелировать из одного в другой минимум многоямной потенциальной поверхности внутренней углеродной стенки. Однако эта задача была решена в общем виде с использованием модельного гамильтониана в предположении, что потенциальная поверхность движения атома-гостя имеет двадцать минимумов, каждый из которых расположен над центром одного из шестиугольников. При этом природа химического взаимодействия углеродной стенки с атомом-гостем не рассматривалась.
Данная работа посвящена вопросу изучения эффектов нежестскости атомного остова эндоэдральных комплексов и влияния способов координации атомов-гостей внутри фуллереновой сферы на электронную структуру этих соединений.

Методы и объекты исследования

Электронная и атомные структуры и динамические свойства ряда комплексов фуллерена с атомами лития, гелия и молекулой водорода исследовались стандартными полуэмпирическими квантово-химическими методами PM3, MNDO и INDO, неэмпирическим методом Хартри-Фока и методом молекулярной динамики на основе соответствующих потенциалов. Были рассмотрены следующие объекты:
- Молекула C60, электронная структура и равновесная геометрия рассчитывались в приближении ограниченного метода Хартри-Фока неэмпирическим методом Хартри-Фока в базисе 3-21G и полуэмпирическим методом PM3, молекулярная динамика рассчитывалась в потенциале полуэмпирического метода PM3.
- Ван-дер-ваальсовый димер (C60)2, электронная структура и равновесная геометрия рассчитывались в приближении ограниченного метода Хартри-Фока полуэмпирическим методом PM3, молекулярная динамика рассчитывалась в потенциале полуэмпирического метода PM3.
- Молекула C36, электронная структура и равновесная геометрия рассчитывались в приближении ограниченного метода Хартри-Фока неэмпирическим методом Хартри-Фока в базисе 3-21G и полуэмпирическим методом PM3, молекулярная динамика рассчитывалась в потенциалах полуэмпирического метода PM3 и неэмпирическом потенциале 3-21G.
- Эндоэдральный комплекс Li2@C60, электронная структура и равновесная геометрия рассчитывались в приближении ограниченного метода Хартри-Фока полуэмпирическим методом MNDO, молекулярная динамика рассчитывалась в потенциале полуэмпирического метода MNDO.
- Экзоэдральный комплекс Li2C60, электронная структура и равновесная геометрия рассчитывались в приближении ограниченного метода Хартри-Фока полуэмпирическим методом MNDO, молекулярная динамика рассчитывалась в потенциале полуэмпирического метода MNDO.
- Эндо-экзоэдральный комплекс Li [Li@C60] (один из ионов находится внутри сферы, а другой - снаружи), электронная структура и равновесная геометрия рассчитывались в приближении ограниченного метода Хартри-Фока полуэмпирическим методом MNDO, молекулярная динамика рассчитывалась в потенциале полуэмпирического метода MNDO.
- Ван-дер-ваальсовый димер (Li2@C60)2 (два эндоэдральных комплекса Li2@C60 связаны друг с другом ван-дер-ваальсовыми взаимодействиями). Данный фрагмент является кластерной моделью молекулярного твердого тела, которое формирует эндоэдральный фуллерен. Электронная структура и равновесная геометрия рассчитывались в приближении ограниченного метода Хартри-Фока полуэмпирическим методом MNDO, молекулярная динамика рассчитывалась в потенциале полуэмпирического метода MNDO.
- Эндоэдральный комплекс Li@C60+, электронная структура и равновесная геометрия рассчитывались в приближении ограниченного метода Хартри-Фока полуэмпирическим методом MNDO, молекулярная динамика рассчитывалась в потенциале полуэмпирического метода MNDO.
- Эндоэдральный комплекс H2@C36, электронная структура и равновесная геометрия рассчитывались в приближении ограниченного метода Хартри-Фока неэмпирическим методом Хартри-Фока в базисе 3-21G и полуэмпирическим методом PM3, молекулярная динамика рассчитывалась в потенциалах полуэмпирического метода PM3 и неэмпирическом потенциале 3-21G.
- Эндоэдральный комплекс H2@C50, электронная структура и равновесная геометрия рассчитывались в приближении ограниченного метода Хартри-Фока полуэмпирическим методом PM3, молекулярная динамика рассчитывалась в потенциалах полуэмпирического метода PM3.
- Эндоэдральный комплекс H2@C60, электронная структура и равновесная геометрия рассчитывались в приближении ограниченного метода Хартри-Фока полуэмпирическим методом PM3, молекулярная динамика рассчитывалась в потенциалах полуэмпирического метода PM3.
- Ряд эндоэдральных комплексов Hen@C60, n=2, 3,4 электронная структура и равновесная геометрия рассчитывались в приближении ограниченного метода Хартри-Фока полуэмпирическим методом INDO, молекулярная динамика рассчитывалась в потенциале полуэмпирического метода INDO.
Все расчеты проводились без учета симметрии системы. Оптимизация геометрии этих комплексов проводилась во всех методах с параметром сходимости 0.01 ккал/моль/атом.
В настоящее время метод неэмпирической молекулярной динамики [38], не требующий введения эмпирических межмолекулярных и межатомных потенциалов для расчетов, широко используется для исследований динамических свойств молекулярных систем. В этом подходе электронная система описывается набором волновых функций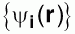 , которые принадлежат основному состоянию потенциальной поверхности Борна-Оппенгеймера в любой момент времени. Такой подход позволяет описать совместное движение электронов и ядер, которые описываются набором координат , которые принадлежат основному состоянию потенциальной поверхности Борна-Оппенгеймера в любой момент времени. Такой подход позволяет описать совместное движение электронов и ядер, которые описываются набором координат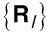 . При этом фиктивная кинетическая энергия электронов остается малой по сравнению с кинетической энергией ионов, что позволяет рассчитывать силы, действующие на ядра в любой момент времени по теореме Гельмана-Феймана для электронных систем, соответствующих мгновенным ядерным конфигурациям. Уравнения движения полной динамической системы, включающей фиктивную электронную динамику и действительную ионную динамику определяются лагранжианом: . При этом фиктивная кинетическая энергия электронов остается малой по сравнению с кинетической энергией ионов, что позволяет рассчитывать силы, действующие на ядра в любой момент времени по теореме Гельмана-Феймана для электронных систем, соответствующих мгновенным ядерным конфигурациям. Уравнения движения полной динамической системы, включающей фиктивную электронную динамику и действительную ионную динамику определяются лагранжианом:
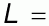 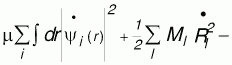
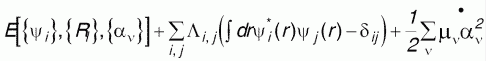
где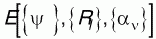 - функционал полной энергии, получаемый в любом квантово-химическом методе, набор - функционал полной энергии, получаемый в любом квантово-химическом методе, набор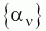 - любые возможные внешние условия - температура, давление, объем и пр., μ- фиктивная масса для электронной динамики, μν - произвольный параметр соответствующей размерности. Матрица - любые возможные внешние условия - температура, давление, объем и пр., μ- фиктивная масса для электронной динамики, μν - произвольный параметр соответствующей размерности. Матрица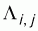 является набором множителей Лагранжа, которые обеспечивают ортонормированность является набором множителей Лагранжа, которые обеспечивают ортонормированность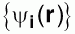 . Из этих уравнений можно получить уравнения движения Эйлера-Лагранжа: . Из этих уравнений можно получить уравнения движения Эйлера-Лагранжа:
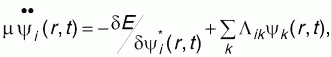
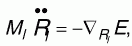
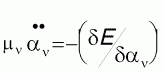 , ,
которые соответственно описывают фиктивную электронную динамику, ионную динамику и влияние внешних условий, например - температуры.
Неэмпирическая молекулярная динамика удовлетворяет приближению Борна-Оппенгеймера только при определенных условиях. Для полупроводников и изоляторов ситуация является простой для выбора μ и других начальных условий. Однако для систем, в которых щель мала, ионы и электроны сильно взаимодействуют. Это приводит к тепловому равновесию между ионами и электронами и к отходу от условий применимости Борна-Оппенгеймера. Для того, чтобы преодолеть эти трудности, в неэмпирической молекулярной динамики используется алгоритм термостатов [39], один для ионов, другой - для электронов. В этом случае имеем:
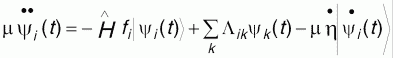 , ,
где fi- число заполнения.
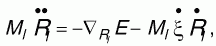
Переменные термостата η и ξ определяются уравнениями:
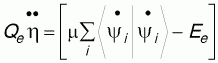 , ,
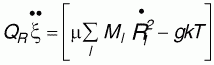 , ,
где Qe и QR - массы термостатов для электронной и ионных частей соответственно, Ee и T - необходимые из условий задачи кинетическая энергия электронов и ионная температура, g - число степеней свободы ионов.
В этом подходе температурные флюктуации, зависящие от времени, включены в уравнения электронного и ионного термостатов, а динамика всей системы подчиняется принципу минимума термодинамического потенциала. Простейший случай ньютоновской динамики описывает движение системы в состоянии равновесия, что позволяет не только исследовать динамические свойства молекулярных и твердотельных систем, но и эффективно находить равновесную атомную структуру.
Следует заметить, что в методе неэмпирической молекулярной механики выполняется закон сохранения энергии во всей системе (термодинамический потенциал), включающей в себя электронный и ионный термостаты, который записывается в следующем виде:
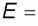 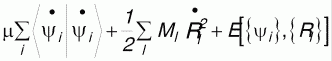
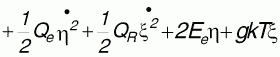 , ,
тогда как энергия электронно-ядерной системы без термостатов из-за температурных флюктуаций не сохраняется. Следовательно, для систем с нежестким атомным остовом возможны ситуации, когда из-за невыполнения закона сохранения энергии температурные условия будут влиять на электронную структуру и спектры исследуемых систем из-за того, что различные атомные конфигурации должны обладать различными электронными спектрами. Так, в частности, из-за быстрых температурных перестроек в электронных спектрах должна наблюдаться суперпозиция спектров, относящихся к различным конфигурациям, что должно выражаться к уширению и заплыванию ряда спектральных особенностей.

Результаты расчетов и их обсуждение

Электронная структура молекулы С60 в настоящее время хорошо известна, известны также и ее динамические свойства в различных условиях и состояниях (см. Табл. 1). Экспериментальное расстояние между углеродными сферами в фуллерите С60 составляет 0.33нм. [40]. Расчет ван-дер-ваальсового димера, моделирующего межмолекулярное взаимодействие в ван-дер-ваальсовом твердом теле, которым является твердый фуллерит, переоценил это расстояние на 0.145 нм. В нашем расчете расстояние между фуллереновыми сферами С60 равно 0.475 нм. Расчеты свободной молекулы С60 показали, что частота ее вращения при 300 К составляет 0.79*1010 сек-1, а частота вращения углеродных сфер в димере (С60)2 - 0.79*109 сек-1. Экспериментальные частоты, определенные по спектрам ЯМР для газообразной молекулы С60 при 300 К составляет - 3.3*1011 сек-1 [28-30], для молекулы С60 при 300 К в твердом теле - 1.1*1011 сек-1, а для С60 ниже 260 К в твердом теле - 5.0*108 сек-1. Как видно, наши теоретические расчеты методом неэмпирической молекулярной динамики качественно повторяют тенденцию уменьшения частот при переходе от газа молекул С60 к твердому телу, хотя количественного согласия нет. Отличия в частотах вращения, очевидно, вызваны тем фактом, что полуэмпирические методы расчета, как правило, завышают энергию и константу связи и, тем самым, недооценивают изменение межъядерных расстояний при увеличении температуры.
Вращение и возникновение ненулевого орбитального момента всей молекулы при повышении температуры объясняется изменением полного электронного орбитального момента. Действительно, полный момент системы (электронный плюс ядерный) должен сохраняться, однако при повышении температуры изменяются эффективные межъядерные расстояния, следовательно в общем виде можно записать:
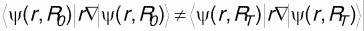 . .
Это неравенство имеет место, поскольку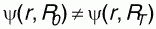 , так как при изменении температуры изменяется набор координат ядер ( , так как при изменении температуры изменяется набор координат ядер (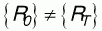 ), которые входят в полноэлектронную волновую функцию в виде параметров. Следовательно, вся система должна компенсировать изменение электронного орбитального момента изменением ионного орбитального момента, что и проявляется во вращении молекул как целого. ), которые входят в полноэлектронную волновую функцию в виде параметров. Следовательно, вся система должна компенсировать изменение электронного орбитального момента изменением ионного орбитального момента, что и проявляется во вращении молекул как целого.
Неэмпирические расчеты низшего фуллерена С36 в базисе 3-21G при температуре 300К показали, что этот эффект воспроизводится и в том случае, когда в методе молекулярной динамики используется потенциал, полученный ab initio методом. Из-за того, что такого типа расчеты требуют очень большого машинного ресурса, оценить частоту вращения молекулы не удалось. Расчет частоты вращения С36 с использованием полуэмпирического потенциала, полученного в рамках метода PM3, показал, что частота вращения несколько выше, нежели чем для С60, и равна 3.2 *1010 сек-1.
Ab initio расчет в базисе 3-21G равновесной атомной структуры гипотетического эндоэдрального комплекса H2@C36 показал, что молекула водорода располагается в центре углеродной сферы. Расчеты методом молекулярной динамики при температуре 300К также продемонстрировали нежесткость координации молекулы Н2 внутри сферы, однако оценить частоту вращения в этом случае также не удалось из-за ограниченности вычислительного ресурса. Расчет молекулярной динамики в полуэмпирическом потенциале РМ3 показал, что молекула водорода вращается внутри сферы с частотой 4*1013 сек-1. При этом следует отметить, что молекула водорода никуда не уходит из центра углеродной сферы.
Расчет динамики гипотетической системы H2@C50 показал, что частота вращения молекулы водорода в этом эндоэдральном комплексе несколько снижается - до 3*1013 сек-1, что объясняется наличием плато на потенциальной поверхности внутри углеродной сферы. Молекула водорода во время движения смещается на 0.09 нм. от центра вдоль длинной оси C50.
Расчет динамики эндоэдрального комплекса H2@C60 при 300К показал, что молекула водорода в нем не вращается, а хаотично двигается внутри сферы за счет температурных флюктуаций, что объясняется наличием большого плато на потенциальной поверхности внутри углеродной сферы во всех направлениях, которое существенно превышает размеры молекулы водорода. Так, смещения молекулы-гостя достигают 0.1 нм. от центра C60. Расчет динамики системы при 4К показал, что амплитуда движений молекулы водорода снижается до 0.01 нм., однако система все равно остается нежесткой.
Расчеты молекулярной динамики других интересных эндоэдральных комплексов фуллеренов с атомами гелия (Hen@C60 , n=2, 3, 4) в полуэмпирическом потенциале INDO показал, что подобные системы остаются нежесткими при Т=4К, причем частоты вращения атомов гелия оцениваются для этих объектов в пределах 3 ÷5*1012 cек-1. Повышение температуры до 300К приводит к заметному (до 6 ÷7*1012 cек-1) повышению частоты вращения гелиев. Необходимо отметить, что внутри углеродной сферы фактически существуют молекулы Hen, причем во всех случаях межъядерное расстояние равно 0.18 нм. (Нужно отметить, что расчет ван-дер-ваальсового димера He2 методом INDO дает межъядерное расстояние 0.50 нм., а в ab initio подходе (базис 6-31G) - 0.32 нм.)
Расчеты электронной и атомной структур комплексов с литием показал, что ионы лития в эндоэдральном комплексе Li2@C60 координируются к противоположным вершинам шестиугольников, лежащих друг против друга таким образом, что ось фрагмента Li2 находится как раз посередине сферы, причем расстояние Li-Li - 0.299 нм, что хорошо совпадает с расстоянием С-С между противоположными углеродами из шестиугольников оснований, а расстояние Li-С (до углеродов, принадлежащих шестиугольникам) - 0.328 нм.
Координация литиев в экзоэдральном комплексе Li2C60 может идти как по центру шестиугольника, так и по центру пятиугольника, причем расстояние от иона лития до атомов углерода шестиугольника составляют 0.232нм, а до атома углерода пятиугольника - 0.234нм.
В эндо-экзоэдральном комплексе Li [Li@C60] экзоэдральный ион координировался к центру шестиугольника с расстоянием Li-С, равным 0.231 нм, а эндоэдральный - к центру шестиугольника, соседствующего с шестиугольником, к которому координируется внешнесферный литий, причем расстояние эндоэдральный литий - атом углерода составляет 0.241нм.
Координация лития в комплексе Li@C60+ происходит по центру одного из шестиугольников, причем расстояние Li-С равно 0.2405 нм, а расстояние ион лития - центр шестиугольника - 0.1909 нм.
Расчет ван-дер-ваальсового димера (Li2@C60)2 показал, что углеродные сферы могут координироваться ребрами пятиугольник-шестиугольник с ближайшими расстояниями углерод-углерод из соседних сфер 0.471 нм. При этом координация литиев внутри сфер сохраняется, а сами литиевые пары в различных сферах располагаются параллельно на расстоянии 1.150 нм друг от друга.
Расчеты методом молекулярной динамики в полуэмпирическом потенциале показывают, что при температуре 4 К эндоэдральные ионы лития в комплексе Li2@C60 «примораживаются» к углеродной стенке. При температуре выше 79 К наблюдается динамический переход, при котором ионы выходят из равновесной геометрии и начинают вращаться внутри сферы с частотой 1.0*1012 сек-1, при этом вращается и сама углеродная сфера с частотой 2.5*109 сек-1. (Необходимо отметить, что эта температура динамического перехода является всего-лишь оценкой высоты потенциального барьера, а не термодинамической характеристикой. Все расчеты, как это уже говорилось выше, проводились методом молекулярной динамики, который не учитывает в полной мере температурные флюктуации и фактически моделирует состояние термодинамического равновесия.) При температуре 300 К частота вращения увеличивается и для литиев она составляет 2.5*1012сек-1 и 3.4*109 сек-1 для углеродной сферы (см. Таблицу 1).
Как показали аналогичные молекулярно-динамические расчеты, экзоэдральный комплекс Li2C60 - жесткий, вплоть до температуры 300 К. Внешние ионы лития только колеблются вблизи своих равновесных геометрий над центрами как шестиугольника, так и пятиугольника.
Поведение эндоэдрального иона в эндоэкзоэдральном комплексе Li [Li@C60] существенно более сложно: при 77 К он меняет свою координацию с центра шестиугольника на ребро шестиугольник-шестиугольник, принадлежащему обеим соседствующим шестиугольникам, к которым при 4 К координировались экзо- и эндоэдральные ионы. При 300 К эндоэдральный ион начинает мигрировать в телесном угле порядка 30° в области координации экзоэдрального лития.
Динамические свойства димера (Li2@C60)2 принципиально не отличаются от таковых для мономера Li2@C60. Введение несимметричного внешнего поля в виде одного ван-дер-ваальсового соседа, что моделирует взаимодействие с одним ближайшим соседом в фуллерите, существенно (примерно до 300К) увеличивает температуру динамического перехода, однако основное свойство - нежесткость атомного остова сохраняется. Ионы лития в каждой сфере движутся независимо от соседней пары с частотой 3.0*1010 сек-1 и взаимная их координация меняется практически произвольным образом в зависимости от времени. Как и в неинтеркалированном фуллерите, в димере наблюдается независимое вращение самих углеродных сфер с частотой 3.1*109 сек-1.
Очевидно, что столь заметное повышение температуры динамического перехода (с 78 до 300К) в димере (Li2@C60)2 по сравнению с мономером Li2@C60 связано с фактическим снятием вырождения потенциала внешнего окружения. Скорее всего адекватный учет ближайшего окружения комплекса Li2@C60 в твердом теле должен заметно понизить эту температуру.
Расчеты методом молекулярной динамики в полуэмпирическом потенциале показывают, что при температуре 300 К эндоэдральный ион лития в комплексе (Li@C60)+ движется с частотой порядка 5*1012 сек-1.
Проследим теперь зависимость электронной структуры от динамических свойств эндоэдрального комплекса Li2@C60. На Рис. 2 представлены полные плотности состояний, построенных для 16 стоп-кадров с интервалом 0.01 ps динамического кино для этого комплекса, рассчитанного при 300К. Как видно, происходит «заплывание» внедренного электронного состояния, образованного за счет дополнительных электронов, поставляемых атомами лития. Изменение энергии верхней заполненной орбитали, обусловленное изменением координации ионов лития под действием температурных флюктуаций, достаточно велико - порядка 1 эВ. Движение ионов лития вызывает и волну поляризации на углеродной сфере. Так, вслед за движением ионов лития меняют свой заряд и атомы углерода, малликеновские заряды которых могут меняться от нескольких сотых единицы электронного заряда до пятнадцати сотых электронного заряда.

Выводы

Таким образом, расчеты методом неэмпирической молекулярной динамики показывают:
- Эндоэдральные комплексы фуллеренов с закрытыми оболочками и атомами-гостями, не связанными ковалентно с углеродными стенками, являются системами нежесткими.
- Это свойство объясняется невысокими (порядка десятков К) потенциальными барьерами на потенциальной поверхности атомных перегруппировок внутри углеродной сферы.
- Движение ионов внутри сферы под действием температурных флюктуаций приводит к размыванию потолка валентной зоны, состоящей из внедренного электронного состояния и к волне поляризации на поверхности углеродной сферы, которая движется вслед за положительно заряженными ионами-гостями.
Работа выполнена в Центре коллективного пользования «Квантово-химические расчеты нанокластеров» Красноярского научно-образовательного центра высоких технологий, созданного на средства ФЦП «Государственная поддержка интеграции высшего образования и фундаментальной науки», грант №69. Авторы благодарят Российский фонд фундаментальных исследований за поддержку в рамках проекта РФФИ № 97-03-33684a, Госпрограмму ВТСП, проект №99019 и Госпрограмму «Фуллерены и атомные кластеры» за поддержку в рамках проекта №97 018, NATO Scientific Affairs Division в рамках проекта PST.CLG 974818.

Список литературы

[1] А. В. Елецкий, Б.М. Смирнов, УФН, 165, 977 (1995).
[2] C.T. White, J.W. Mintmire, R.C. Mowrwy, D.W. Brenner, D.H. Robertson, J.A. Harrison, B.I. Dunlop, Predicting properties of fullerenes and their derivatives, in: Buckminsterfullerenes, edt. By W.E Billups and M.A. Ciufolini, VCH Publishers, Inc.: NY, 1993.
[3] W. Andreoni, Ann. Rev. Phys. Chem., 49, 405 (1998).
[4] A.R. Ramirez, Superconductivity Review, 1, 1&2, 1 (1994)
[5] N. Krawez, A. Gromov, R. Tellgmann, E.E.B. Campbell, Electronic properties of novel materials - Progress in molecular nanostructures, XII International Winterschool, Kirchberg, Tyrol, Austria, 1998, p. 368.
[6] Y. Yoshinari, H. Alloul, V. Brouet, G. Kriza, K. Holczer, L. Forro, Phys. Rev. B54, 6155 (1996).
[7] T. Pichler, M.S. Golden, M. Knupfer, J. Fink, XII International Winterschool Electronic properties of novel materials, Proceedings, edt. by H. Kuzmany, 271 (1998).
[8] D.M. Poirier, M. Knupfer, J.H. Weaver, W. Andreoni, K. Laasonen, M. Parinello, D.S. Bethune, K.Kikuchi, Y. Achida, Phys.Rev. B49, 17403 (1994).
[9] J.H. Weaver, Acc. Chem. Res. 25, 143 (1992).
[10] M.Takata, B.Umeda, E.Nishibori, M.Sakata, Y.Saito, M.Ohno, H.Shinohara, Nature, 377, 46 (1995).
[11] W. Sato, K. Sueki, K. Kikuchi, S. Suzuki, Y. Achiba, H. Nakahara, Y. Ohkubo, K. Asai, F. Ambe, Phys.Rev. B58, p. 10850 (1998).
[12] C. Gu, F. Stepniak, D.M. Poirier, M.B. Jost, P.J. Benning, Y. Chen, T.R. Ohno, J.J.L. Martins, J.H. Weaver, J. Fure, R.E. Smalley, Phys. Rev. В53, 1196 (1995).
[13] J. Chioslovski, E.D. Fleischmann, J. Chem. Phys., 94, 3730 (1991).
[14] А.Б. Ройцин, Л.В. Артамонов, А.А. Климов, ФНТ 23, 1112 (1997).
[15] H. Mauser, T. Clark, A. Hirsch, XII International Winterschool Electronic properties of novel materials, Proceedings, edt. by H. Kuzmany, 202 (1998).
[16] C.G. Joslin, J. Yang, C.G. Gray et.al., Chem. Phys. Let., 211, 587 (1993)
[17] L. Pang, F. Brisse, J. Phys. Chem., 97, 8562 (1993).
[18] Y.S. Li, D. Tomanek, Chem. Phys. Lett., 221, 453 (1994).
[19] D. Tomanek, Y.S. Li, Chem. Phys. Lett., 243, 42 (1995).
[20] В.А. Левашов, А.А. Ремова, В.Р. Белослудов, Письма в ЖЭТФ, 65, 647 (1997).
[21] Y. Maryyama, K. Ohno, K. Esfarjani, Y. Kawazoe, Sci. Rep. RITU A41, 183 (1996).
[22] A.H.H. Chang, W.C. Ermler, R.M. Pitzer, J. Chem. Phys., 94, 5004 (1991).
[23] J. Liu, S. Iwata, Phys. Rev. B50, 5552 (1994).
[24] F. De Proft, C. Van Alsenoy, P. Geerlings, J. Phys. Chem., 100, 7440 (1996).
[25] S. Patchkovskii, W. Thiel, J. Chem. Phys., 106, 1796 (1997).
[26] Y. Wang, D. Tomanek, Chem. Phys. Lett., 208, 79 (1993).
[27] B.I. Dunlop, J.L. Ballester, P.P. Schmidt, J. Phys. Chem., 96, 9781 (1992).
[28] Y. Maniwa, K. Mizoguchi, K. Kume, K. Kikuchi, I. Ikemoto, S. Suzuki, Y. Achida, Solid State Commun., 80, 609 (1991).
[29] R.D. Johnson, C.S. Yannoni, H.C. Dorn, J.R. Salem, D.S. Bethune, Science, 225, 1235 (1992).
[30] R. Tycko, G. Dabbagh, R.M. Fleming, R.C. Haddon, A.V. Makhija, S.M. Zahurak, Phys.Rev.Lett., 67, 1886 (1991)
[31] P.A. Heiney, J.E. Fischer, A.R. McGhi, W.J. Romanov, A.M. Denenstein, J.P. McCauley, Jr., A.B. Smith III, D.E. Cox, Phys. Rev. Lett., 66, 2911 (1991).
[32] R. Moret, P.A. Albouy, V. Agafonov, R. Ceolin, D. Andre, A. Dvorkin, H. Szwarc, C. Fabre, A. Rassat, A. Zahab, P. Bernier, J. Phy. (France) I 2, 511 (1992).
[33] W. Andreoni, A. Curioni, Phys. Rev. Lett., 77, 834 (1996).
[34] W. Andreoni, A. Curioni, Appl. Phys. A66, 299 (1998).
[35] Д.А. Бочвар, Е.Г. Гальперн, ДАН СССР, 209, 610 (1973).
[36] H. W. Kroto et al. Nature, 318, 162 (1985).
[37] J.L. Ballester, B.I. Dunlop, Phys. Rev. A45, 7985 (1992).
[38] R. Car, M. Parinello, Phys. Rev. Lett., 55, 2471 (1985).
[39] P.E. Bloechl, M. Parinello, Phys. Rev. B45, 9413 (1992).
[40] W. Krдtschmer et al, Nature 347, 354 (1990).

Таблица 1

Частоты вращения димера Li2 фуллерена С60 в эндоэдральных комплексах Li2@C60 и (Li2@C60)2.
| Соединение, температура | Частота вращения димера Li2, сек-1 | Частота вращения фуллерена С60, сек-1 |
| Li2@C60 при Т=79 К | 1*1012 | 2.5*109 |
| Li2@C60 при Т=300 К | 2.5*1012 | 3.4*109 |
| (Li2@C60)2 при Т=300 К | 3.0*1010 | 3.1*109 |
| С60 при Т=300 К | - | 7.9*109 |
| (С60)2 при Т=300 К | - | 7.9*108 |
| Экспериментальная частота вращения газообразной молекулы С60 при 300 К [28-30] | - | 3.3*1011 |
| Экспериментальная частота вращения молекулы С60 в фуллерите при 300К [28-30] | - | 1.1*1011 |
| Экспериментальная частота вращения молекулы С60 в фуллерите ниже 260 К [28-30] | - | 5.0*108 |

Рисунки

Рис. 1. Фотоэлектронные (PES) спектры и спектры обращенной фотоэмиссии (IPES) [9] соединений типа KxC60. При x=1 спектральная интенсивность фотоэлектронного спектра на уровне ферми мала, а первая особенность спектра обращенной фотоэмиссии большая, однако с ростом степени допирования интенсивность фотоэлектронного спектра возрастает, а первой особенности спектра обращенной фотоэмиссии - падает.
Рис. 2. Электронная структура 16 стоп-кадров динамического кино, наложенных друг на друга и сделанных с шагом 0.01 ps рассчитанного для комплекса Li2@C60 при температуре 300К. Видно, что верхняя заполненная орбиталь (внедренное электронное состояние) меняет свое положение с амплитудой 1 эВ. На вставке изображено увеличенное внедреное состояние.
|