
Теория сверхпроводящей фазы сильно коррелированных электронов с учетом вкладов от аномальных компонент силового оператора

Головня Александр Александрович
лаборатория Теоретической физики
Института физики им. Л.В. Киренского СО РАН
(тезисы доклада)
Хорошо известно, что высокотемпературные сверхпроводники (ВТСП) принадлежат к системам с сильными электронными корреляциями (СЭК). Прежде всего это подтверждается тем, что в недопированном случае медно-оксидные соединения являются антиферромагнитными диэлектриками, тогда как с точки зрения обычной зонной теории они должны были бы быть металлами. При дырочном или электронном легировании происходит разрушение дальнего магнитного порядка с последующим возникновением сверхпроводящей фазы, если температура . В области плохого металла система проявляет не ферми-жидкостное поведение. Эти факторы при попытках их теоретической интерпретации стимулировали привлечение моделей, в которых кулоновское взаимодействие между электронами играет существенную роль. Наиболее популярными с этой точки зрения являются: модель Хаббарда, модель Эмери, а также модели, полученные на их основе в режиме СЭК (t-J- и t-J*- модели).
При теоретическом описании сверхпроводящей фазы сильно коррелированных систем в рамках эффективных гамильтонианов чаще всего используются два метода: диаграммная техника для операторов Хаббарда (ДТХ) и метод двухвременных неприводимых функций Грина (ФГ). Во втором подходе процедура выделения неприводимых частей в высших ФГ с введением аномальных составляющих приводит к уравнениям типа уравнений Горькова. При этом в теорию входит ренормированный спектр фермиевских возбуждений, существенно зависящий от магнитных корреляторов. Если сверхпроводящая фаза описывается на основе эффективного гамильтониана, выведенного из модели Хаббарда в режиме сильных корреляций, то существенным оказывается учет трехцентровых взаимодействий (t-J*-модель).
В рамках второго метода приходится учитывать хорошо известную особенность ДТХ, заключающуюся в наличии концевых диаграмм. Их полная совокупность формирует силовой оператор. В работе впервые показано, что при описании сверхпроводящей фазы методом ДТХ в диаграммном ряду возникают аномальные концевые диаграммы, определяющие аномальные компоненты силового оператора 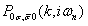 . В этой связи представляется актуальным вывод уравнений самосогласования, их решение и анализ условий реализации сверхпроводящей фазы с различной симметрией параметра порядка. . В этой связи представляется актуальным вывод уравнений самосогласования, их решение и анализ условий реализации сверхпроводящей фазы с различной симметрией параметра порядка.
В работе для t-J*-модели при учете аномальных компонент массового и силового операторов получено точное представление для матричной одночастичной функции Грина. В однопетлевом приближении вычислены все аналитические вклады для нормальных 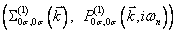 и аномальных компонент и аномальных компонент 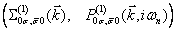 массового и силового операторов. Зависимость компонент силового оператора от мацубаровских частот привела к тому, что сверхпроводящая фаза стала описываться бесконечной системой интегральных уравнений. Анализ этой системы проведен при учете перескоков между узлами, находящимися в пределах трех координационных сфер. При выводе уравнения, определяющего влияние трехцентровых взаимодействий на концентрационную зависимость Tc(n) , отмеченная бесконечная система интегральных уравнений в аналитическом виде решена точно. Это позволило сравнительно простым образом проанализировать уравнение для критической температуры перехода в сверхпроводящую фазу с различной симметрией параметра порядка. На основе численных расчетов показано, что учёт массового и силового операторов. Зависимость компонент силового оператора от мацубаровских частот привела к тому, что сверхпроводящая фаза стала описываться бесконечной системой интегральных уравнений. Анализ этой системы проведен при учете перескоков между узлами, находящимися в пределах трех координационных сфер. При выводе уравнения, определяющего влияние трехцентровых взаимодействий на концентрационную зависимость Tc(n) , отмеченная бесконечная система интегральных уравнений в аналитическом виде решена точно. Это позволило сравнительно простым образом проанализировать уравнение для критической температуры перехода в сверхпроводящую фазу с различной симметрией параметра порядка. На основе численных расчетов показано, что учёт 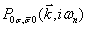 приводит к существенному изменению области реализации сверхпроводящей фазы. Этот факт должен приниматься во внимание при теоретической интерпретации экспериментальных данных по допированным медно-оксидным соединениям с высокими значениями температуры сверхпроводящего перехода. приводит к существенному изменению области реализации сверхпроводящей фазы. Этот факт должен приниматься во внимание при теоретической интерпретации экспериментальных данных по допированным медно-оксидным соединениям с высокими значениями температуры сверхпроводящего перехода.
Фоторепортаж
|