Проведено обобщение диаграммной техники для операторов Хаббарда на случай учета трехцентровых взаимодействий. Эти взаимодействия появляются, например, при построении эффективного гамильтониана H_eff для модели Хаббарда в режиме сильных электронных корреляций. В этом случае H_eff действует в усеченном гильбертовом пространстве, не содержащем двухэлектронных конфигураций на одном узле, и состоит из двух слагаемых: H_eff = H_t-J + H₍₃₎. H_t-J является гамильтонианом t-J модели, а слагаемое H₍₃₎ соответствует учету трехцентровых взаимодействий. В мацубаровском представлении записана замкнутая система уравнений для нормальной и аномальной функции Грина, включающая аномальные компоненты массового оператора. Для всех необходимых компонент массового оператора получено диаграммное представление и вычислен соответствующий аналитический вклад. Решение системы уравнений Горькова позволило записать для сверхпроводящего параметра порядка интегральное уравнение, учитывающее вклады от трехцентровых взаимодействий. Оказалось, что эти взаимодействия сильно уменьшают область реализации сверхпроводящего состояния с d_x2-y2 - типом симметрии параметра порядка.

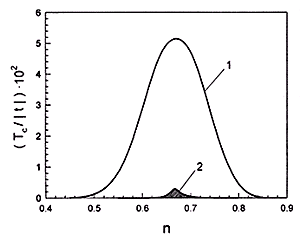На представленном рисунке кривая 1 описывает зависимость температуры перехода T_c в сверхпроводящее состояние без учета трехцентровых взаимодействий. Кривая 2 отражает ту же самую зависимость, но при включении этих взаимодействий. Видно, что роль трехцентровых слагаемых эффективного гамильтониана является весьма существенной для последовательного описания высокотемпературных сверхпроводников.

• Вальков В.В., Валькова Т.А., Дзебисашвили Д.М., Овчинников С.Г.
  Сильное влияние трехцентровых взаимодействий на формирование сверхпроводимости d_x2-y2 -симметрии в t-J*-модели. Письма в ЖЭТФ, т.76, вып.8, стр. 450-454 (2002).

Методом диаграммной техники для операторов Хаббарда изучено влияние трехцентровых взаимодействий на условия реализации сверхпроводящего состояния с d-типом симметрии параметра порядка. Показано, что учет трехцентровых взаимодействий для типичных значений параметров модели приводит к уменьшению температуры сверхпроводящего перехода в десятки раз. (совместно с лабораторией ФМЯ).

Рассмотрен стационарный эффект Джозефсона в двойной барьерной структуре. Проанализирована зависимость критического тока от расстояния между барьерами и от температуры. Показано, что при резонансном расстоянии между барьерами температурная зависимость критического тока отличается от нерезонансного случая, так что характер изменений зависит от геометрии контакта.

Развит многочастичный подход для описания спин-зависящего транспорта в квантовых системах типа дотов. Для таких систем, моделируемых гамильтонианом Андерсона с двумя зонами проводимости показано существование спин-зависящей ренормировки локализованных уровней. В результате возникает резкое уменьшение туннельного тока для ферромагнитно упорядоченных каналов по сравнению с парамагнитным состоянием каналов. Отмечено, что рассмотренная система проявляет черты спин-зависящего резонансного туннелирования для ферромагнитно упорядоченных каналов.

Спиновая система в модели Гейзенберга (S = 1/2) на квадратной решетке с антиферромагнитным (AF) обменным взаимодействием между ближайшими соседями, в которой дальний магнитный порядок при любых T≠0 отсутствует, рассмотрена как пространственно однородная и изотропная спиновая жидкость (SL). Описание проведено методом двухмерных температурных функций Грина в рамках теории второго порядка. Показано, что при Т→ 0 SL, не меняя симметрии, переходит в синглетное состояние с энергией (на связь) ε₀ = -0.352, причем корреляционная длина ξ∝ Т^-1exp(Т₀/T) расходится. Пространственные спиновые корреляторы знакопеременны, как и в AF состоянии. Теория позволяет вычислить основные характеристики системы во всей температурной области.

Рассмотрена стабилизация антиферромагнитного упорядочения в гейзенберговской модели с s = 1/2 для ГЦК решетки за счет анизотропии обменного взаимодействия. Получена теоретическая зависимость, определяющая величину температуры магнитного упорядочения при различных значениях параметра анизотропии. На основании этой зависимости и экспериментального значения TN определено как отношение констант обменного взаимодействия для продольных и поперечных спиновых компонент, так и сами величины этих констант. (совместно с лабораторией ФМЯ).

Рассмотрена проблема основного состояния для модели Гейзенберга с антиферромагнитным обменным взаимодействием между ближайшими соседями с величиной спина s = 1/2, расположенными в узлах ГЦК решетки. Показано, что для такой системы из-за фрустрированных обменных связей и квантовых спиновых флуктуаций дальний антиферромагнитный порядок отсутствует. Поэтому основным состоянием становится состояние квантовой спиновой жидкости. Для описания этой фазы развита линейная теория второго порядка и доказано, что при Т = 0 квантовая спиновая жидкость находится в состоянии спинового синглета. Рассчитаны термодинамические свойства спиновой жидкости в ГЦК решетке во всем температурном диапазоне и характер пространственных спиновых корреляций.

Для описания слабого антиферромагнетизма рутенокупрата RuSr₂GdCu₂O₈ рассмотрена t-J-I модель с взаимодействием Дзялошинского. В этой модели для слабодопированного режима при учете сильных корреляций получены и решены линеаризованные уравнения движения для функций Грина, описывающих двухподрешеточную скошенную фазу. В аналитическом виде определены выражения для спектра квазичастиц и собственных состояний. (совместно с лабораторией ФМЯ).

Работы выполнены при поддержке:

• Гранта РФФИ № 00-02-16110
• Гранта РФФИ-ККФН ("Енисей") № 02-02-97705
• Программы РАН "Квантовая макрофизика"
• ФЦП "Интеграция": проекты № Б001/850, №Я0007/2303
• Благотворительного фонда содействия отечественной науки

Лаборатория теоретической физики