Впервые теоретически исследовано влияние смеси одно- и трёхмерных неоднородностей на спектр волн в сверхрешетке. Показано, что спадающая часть корреляционной функции сверхрешетки имеет форму произведения спадающих частей корреляционных функций компонент смеси. Это приводит к неаддитивности вкладов компонент различной размерности в результирующую модификацию параметров волнового спектра (затухание волн для смеси меньше суммы затуханий, обусловленных отдельными компонентами смеси и т. д.).

1. Ignatchenko V. A., Mankov Yu. I., Maradudin A. A. Effects of the dimensionality of inhomogeneities on the wave spectrum of superlattices. Phys. Rev. B, 68, 024209-1 - 024209-7 (2003).
2. Ignatchenko V. A., Mankov Yu. I., Maradudin A. A. Effects of the mixture of one- and three-dimensional inhomogeneities on the wave spectrum of superlattices. Письма в ЖЭТФ, 77, 335-340 (2003).

Показано, что явный учет особенностей алгебры операторов Хаббарда приводит к наличию сингулярной (при ω=0) составляющей в полной спектральной интенсивности аномальной корреляционной функции

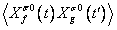
сверхпроводников с электронным механизмом спаривания, а спектральная теорема приобретает вид сингулярного интегрального уравнения

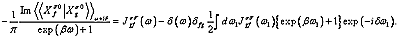
В итоге, учет отмеченной сингулярной составляющей снял существовавший в течении ∼10 лет противоречивый результат о запрете на реализацию сильно коррелированной сверхпроводящей фазы с S-типом симметрии параметра порядка Δ(k) . Для этой симметрии проанализировано решение уравнения самосогласования, выходящее за рамки приближения ближайших соседей.

1. Вальков В.В., Дзебисашвили Д.М., Кравцов А.С. Спектральные представления и проблема описания сверхпроводящего состояния с S-типом симметрии параметра порядка Δ(k). Письма в ЖЭТФ, т.77, вып. 9, с. 604-608 (2003).
2. Вальков В.В., Дзебисашвили Д.М., Кравцов А.С. Особенности спектральной теоремы в теории сверхпроводников c сильными электронными корреляциями. ДАН, т. 93, № 2 (2003).

Исследовано влияние взаимных корреляций неоднородностей различных размерностей на волновой спектр сверхрешётки. Предложен вид корреляционной функции, учитывающий взаимную корреляцию между модулями функций различной размерности при отсутствии взаимной корреляции между самими функциями.

Теоретически исследована форма резонансной линии магнитного резонанса и спиновых волн в ферромагнетике со случайно-неоднородной величиной магнитной анизотропии. Рассматриваются одно- и трёхмерные неоднородности. Процессы многократного рассеяния волн учитываются в рамках приближения когерентного потенциала. Предложен метод приближённого решения интегрального уравнения когерентного потенциала. Получены приближённые аналитические выражения для функции Грина, справедливые в широкой области значений параметров системы. Рассчитаны эффекты обменного сужения резонансной линии во всей области значений корреляционного радиуса неоднородностей.

Показано, что явный учет особенностей алгебры операторов Хаббарда приводит к наличию сингулярной (при ω=0) составляющей в полной спектральной интенсивности аномальной корреляционной функции сверхпроводников с электронным механизмом спаривания, а спектральная теорема приобретает вид сингулярного интегрального уравнения. Учет этой сингулярной добавки приводит к выполнению правила сумм и снимает необоснованный запрет на реализацию S-типа симметрии параметра порядка. Для этой симметрии проанализировано решение уравнения самосогласования, выходящее за рамки приближения ближайших соседей.

Рассмотрено влияние перескоков электронов в дальние координационные сферы на квазиимпульсную зависимость сверхпроводящего параметра порядка. Показано, что учет параметров t2 и t3 существенно улучшает согласие между экспериментальной и теоретической зависимостями критической температуры от степени допирования.

Проведено самосогласованное вычисление температурных и концентрационных зависимостей магнитных корреляторов в t-J* модели при учете трехцентровых взаимодействий в состоянии проводящей квантовой спиновой жидкости. Это позволило определить как непосредственное влияние трехцентровых взаимодействий на неустойчивость нормальной фазы, так и через SU(2) - инвариантные магнитные флуктуации в подсистеме спиновых степеней свободы.

В рамках t-J модели рассмотрено влияние межслойных перескоков на фазовую диаграмму сверхпроводящего состояния бислойных ВТСП. Для d-симметрии ПП показано, что характерный "колокол" концентрационной зависимости критической температуры T_c(n) при достаточно больших значениях интеграла межслойных перескоков t^⊥ имеет два максимума. Такое поведение связывается с удвоением особенности Ван Хова в плотности состояний спектра нормальной фазы. Для s-симметрии влияние межслойных перескоков мало и, в зависимости от t^⊥ , может как повысить, так и понизить величину максимальной T_c.

На основе точного решения задачи об электронном энергетическом спектре двухэлектронной системы в модели Хаббарда, t-J и t-J* моделях проанализирован переход к сокращенному описанию электронной системы модели Хаббарда посредством построения эффективного гамильтониана, действующего в гильбертовом пространстве, не содержащем двух электронов на одном узле. Для всех трех моделей получены дисперсионные уравнения для нахождения энергетического спектра. При этом показано, что в режиме сильных электронных корреляций (U >> t) корректность перехода к описанию системы на основе эффективного гамильтониана имеет место (при U>>t) только по отношению к t-J* модели, в которой (по сравнению с t-J моделью) учитываются трехцентровые взаимодействия (коррелированные перескоки электронов между узлами кристаллической решетки). Отбрасывание же слагаемых эффективного гамильтониана, соответствующих коррелированным перескокам приводит не только к формально иному виду дисперсионного уравнения, но и (при определенных соотношениях между параметрами гамильтониана) к нефизическому результату - возникновению связанного состояния. Полученные результаты однозначно указывают, что при рассмотрении низкоэнергетического спектра сильно коррелированных сверхпроводящих купратов учет трехцентовых взаимодействий, обычно отбрасываемых при переходе к эффективному гамильтониану, имеет принципиальный характер.

Выполнен анализ электронной структуры, магнитных и сверхпроводящих фаз в рутенатах в рамках t-J-I модели с конкуренцией ферромагнитного (I) и антиферромагнитного (J) обменов. Предложена многозонная модель электронной структуры с учетом сильных электронных корреляций, объясняющая сложную фазовую диаграмму и переходы металл-диэлектрик в системах Sr_2-xCa_xRuO₄. Показано, что фрустрации в гцк решетке спинов подавляют антиферромагнитное упорядочение в двойном рутенате Sr₂YRuO₆, для стабилизации которого достаточно малой анизотропии или слабого обменного взаимодействия со вторыми соседями.

Предложен общий подход к построению диссипативной макроскопической динамики на основе микроскопических уравнений движения. Исходя из уравнений Лиувилля (консервативная динамика) получены: поправка к уравнениям Навье-Стокса вязкой жидкости, нелинейное уравнений Фокера-Планка, уравнения гидродинамики в поле самосогласованной силы, уравнение диффузии.

Работы выполнены при поддержке:

• Гранта РФФИ № 00-02-16110
• Гранта ККФН-РФФИ № 02-02-97705 ("Енисей")
• Программы Президиума РАН "Квантовая макрофизика"
• Благотворительного Фонда содействия отечественной науке
• Лаврентьевского конкурса молодежных проектов СО РАН

Лаборатория теоретической физики